Properties of the Fourier Transform Operator
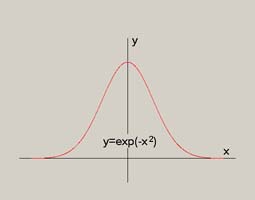
Many people are familiar with the famous bell shaped curve of statistics. (It is the result of the “central limit theorem” – and beloved by quants who managed to crash the economy by ignoring the caveats in its derivation. It is also the solution of the harmonic oscillator in quantum mechanics.) It has always seemed interesting that the Fourier transform of the Gaussian is another Gaussian:
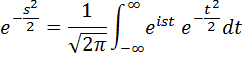
Here I have chosen the Gaussians so that the one on the left is the same as the one on the right. (If the Gaussian on the right is made narrower, the one on the left is wider etc.)
I choose to normalize the Fourier transform with ![]() for reasons of simplification of the equations below.
for reasons of simplification of the equations below.
We (that is myself and whoever is reading this) define the Fourier transform of a function f as follows:
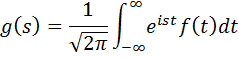
We can write this in the compressed form:
![]()
Here F represents (1/![]() thought of as an operator, and the product of F and f implies an integral in analogy with matrix multiplication (wherein the product implies a sum).
thought of as an operator, and the product of F and f implies an integral in analogy with matrix multiplication (wherein the product implies a sum).
The inverse Fourier Transform is:
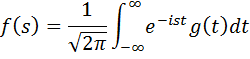
And we can write the inverse Fourier operator as
![]()
Now we see why the normalization is 1/![]() .)
.)
The inverse transform can be simply written:
![]()
Now to return to the subject of the Gaussian, in the language of operator algebra it is an eigenfunction of the Fourier transform and in fact of eigenvalue 1. We are led to ask what might other eigenfunctions of F be, and what are their eigenvalues:
![]()
The product of two Fourier transforms leads to a delta function:
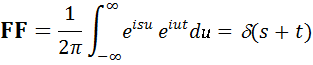
This operator just replaces t with -s in the argument of a function to which it is applied.
Finally ![]() is just the inverse transform and
is just the inverse transform and ![]() is the identity operator:
is the identity operator:
![]()
![]()
This last expression implies that the eigenvalues of the Fourier transform are all forth roots of one, that is: 1, i, -1, -i.
Just as we can find the even and odd parts of any function we can find the parts of any function which are eigenfunctions with the four eigenvalues:
![]()
![]()
![]()
![]()
And therefore:
![]()
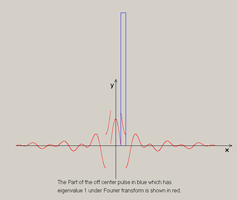
So if we want to find a function which is an eigenvector of the Fourier transform we may apply any of the above to derive an eigenfunction. Unfortunately, most of these functions look pretty silly: Take for example the square pulse,
![]()
Its Fourier transform is
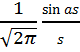
Therefor the eigenfunction ![]() is just ½ the sum of the pulse and its transform, certainly nothing as elegant as the Gaussian.
is just ½ the sum of the pulse and its transform, certainly nothing as elegant as the Gaussian.
Here are some Fourier eigenfunctions which have eigenvalue 1 and are (in my opinion) rather nice:
![]()
![]()
And most amazingly with eigenvalues ![]() Where
Where ![]() are the Hermite polynomials.):
are the Hermite polynomials.):
![]()